
La base 1O sera notre point de départ pour mettre en place les autres bases.
On dispose de 10 symboles : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Exemple 1 : Le nombre 386 vous le comprenez aisément, le 3 est le chiffre des centaines, 8 celui des dizaines et 6 celui des unités.
Pour comprendre la suite du cours il faut écrire 386 autrement : 386= 3×102 + 8×101 + 6×100
En informatique nous utilisons plusieurs bases, mais nous nous limiterons a la base 2 pour écrire des entiers naturels.
Le binaire est le système de numération à la source de la conception d'un ordinateur. Les composants d'un ordinateur fonctionnent
grâce au courant électrique. L'information est donc à deux états : présence de courant 1 et absence de courant 0.
En binaire les rangs sont appelés bit, qui est la contraction de "binary digit" ("chiffre binaire"). Par exemple, le
nombre 10011 ocupe 5 bits. Là où tout se complique, c'est que chaque rang en binaire ne peut avoir que deux
valeurs (binaire = base 2) différentes : 0 ou 1.
Pour la base 10, chaque rang représente une puissance de 10, pour la base 2, chaque
rang occupe une puissance de 2.
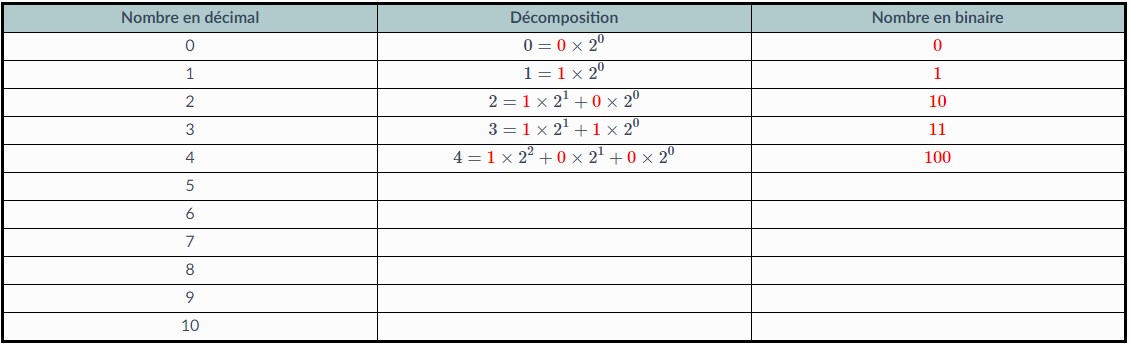
exercice2: Observer et compléter le tableau suivant qui va vous faire compter en binaire jusqu'à 10 :
Voici une video pour vous aider
La video ci-dessous vous explique comment passer de la base 10 vers la base 2
Vous avez maintenant compris la signification d'une écriture en binaire. Reste à mettre en place un algorithme qu nous permettent de faire la conversion d'un nombre écrit en base 10 en base 2. La division euclidienne, celle que vous avez apprise en CM1, va nous permettre d'établir une méthode de conversion de la base 10 vers la base 2. Cette méthode nous permettra d'écrire un algorithme de conversion aisément.
L'écriture binaire de 586 est donc 1001001010
on ajoute les valeurs des bits multiplié par 2 à la puissance la position du bit.
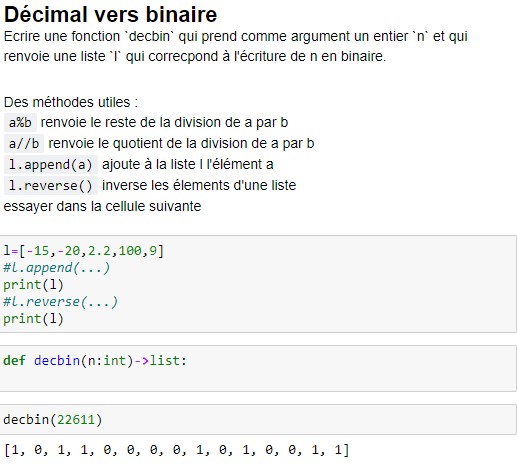
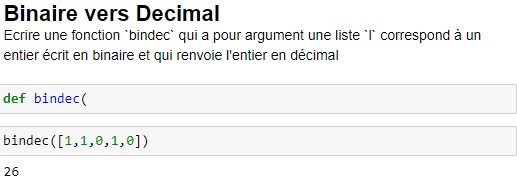
L'objectif de ce TP est la réalisation de fonctions de conversion de binaire en décimal et réciproquement
B2 - Les entiers naturels en binaire
Ci-joint la correction video de la partie decimal vers binaire dans la partie 4.
04/12 eval B1: conversion binaire/decimal, decimal/binaire sur feuille et sur les algorithmes de conversion
Une première idée serait de coder le signe + par un 0 et le signe - par un 1. Ainsi 6 10 = 110 2 se coderait alors en 0110 2. Mais −6 10 se coderait alors en 1110 2
Par conséquent nous allons devoir pous fixer un nombre de bits, n, un espace mémoire. On conserve alors le premier pour le signe et les n −1 autres pour le codage de la valeur absolue du nombre.
Ainsi sur 8 bits −6 10 se code en 1|0000110
Un premier problème avec cette représentation est que le chiffre 0 10 a deux représentations. En effet sur 3 bits: 0 10 = 0|00 2 et 0 10 = 1|00 2
Un autre problème se pose avec cette méthode sur l'addition de deux nombres en binaires.
La représentation d'un nombre entier naturel en binaire se fait de la même manière que dans le paragraphe précédent.
Si on dispose de n bits, le premier sera 0 pour indiquer que l'entier est positif. Et les n − 1 autres seront le codage en binaire de l'entier.
Cela signifie aussi que si l'on dispose de n bits, nous ne pourrons pas dépasser un entier plus grand que 2 n−1 − 1 . Puisque nous ne disposons que de n − 1 bits.
Rappelez vous que sur n bits un entier naturel ne pouvait pas dépasser 2 n − 1. Quand nous codons des entiers relatifs, nous ne pourrons pas dépasser 2 n − 1 − 1 sur n bits.
Pour représenter un entier négatif nous allons utiliser le "complément à deux": Voila la procédure :

Il faut bien distinguer le nombre binaire de sa représentation en binaire.
12 10 = 1100 2 mais en représentation en complément à 2 sur 4 bits 1100 2 = −4
C'est le cas puisque le premier bit est réservé au signe de l'entier.